Finite Elemente Methode (FEM) / Finite-Elemente-Analyse (FEA) / lineare und nichtlineare Analyse
Was ist eigentlich FEM und FEA? Was bedeutet lineare und nichtlineare Analyse? Was sind die Vorteile und in welchen Bereichen kann es angewandtwerden und vor allem wie lässt es sich in die Konstruktion integrieren?
Dafür stehen FEM und FEA
FEM ist die Abkürzung für Finite-Elemente-Methode, FEA bedeutet Finite-Elemente-Analyse.
FEA ist die praktische Anwendung der Finite-Elemente-Methode (FEM) und stehen im Kern für ein numerisches Verfahren zu bestimmten rechnerischen Simulationen. Dabei soll analysiert werden, wie sich feste Körper (also beispielsweise Bauteile) unter definierten Bedingungen verhalten. Um das zu erreichen, erfolgt eine Aufteilung der Körper in eine „finite“ (also endliche) Zahl an Elementen.
Das sind die Vorteile von FEM/FEA
FEM Simulationen bieten eine enorme Unterstützung im Entwicklungsprozess. Sie ergänzen klassische Bauteilprüfungen, die die Gesamtheit und Komplexität der Realität abbilden. Mithilfe der Simulation können im virtuellen Raum Tests durchgeführt werden, die im Realversuch zu kostentreibend oder aufwendig im Aufbau sind. Ein großer Vorteil liegt darin, dass sich praktisch alles am Bildschirm simulieren lässt. Die Bandbereite an möglichen physikalischen Einflüssen reicht von mechanischer Kraft und Temperatur(-unterschieden) bis hin zu elektrischer Spannung und Magnetfeldern. Die Verschiebung sogenannter Knoten, welche die einzelnen Elemente bestimmen, zeigt die Auswirkungen (etwa Verformungen) an.
Typische Anwendungsbereiche von FEM und FEA
Aus den geschilderten Simulationsmöglichkeiten ergibt sich ein breites Anwendungsfeld. So setzen unterschiedliche Branchen wie Maschinenbau, Luftfahrt und Medizintechnik auf entsprechende Software. Auch bei der Planung von Gebäuden kommt sie zum Einsatz – hier ersetzt das Bauwerk das Bauteil. Die vielleicht allgemein bekannteste Anwendung kommt aus dem Automobilbereich: der Crash-Test. Das ist aber nur eines von unzähligen Anwendungsbeispielen aus der Fahrzeugindustrie.
Vorteile durch Integration in die Konstruktion
Um der Finite-Elemente-Analyse zur Verfügung zu stehen, müssen die mittels CAD erstellten Bauteile lediglich in die Software importiert werden. Die Vorteile durch FEA in der Produktentwicklung liegen auf der Hand. Mögliche Fehlkonstruktionen lassen sich bereits in einem frühen Stadium erkennen. Virtuelle Prototypen sorgen dafür, dass ihre realen (und oft kostenintensiven) Pendants erst dann zum Einsatz kommen, wenn die digitalen Möglichkeiten weitgehend ausgeschöpft sind und entsprechende Anpassungen bereits vorgenommen wurden. Zudem lässt sich in kurzer Zeit und ohne großen Aufwand die wichtige Frage klären, welche Auswirkungen eine Anpassung oder Veränderung des Designs mit sich bringt, etwa auf die Leistung oder die Kosten.
Das Problem der Linearität
Das numerische Modell einer Komponente ist immer auch eine Vereinfachung. Hier kommt die sogenannte Linearitätsannahme ins Spiel. Ein typisches Beispiel aus der Konstruktionswelt: Es wird angenommen, dass eine Verdopplung der Last zu einer Verdopplung der Durchbiegung führt. Die Verdopplung der Durchbiegung wiederum führt zu einer Verdopplung des Spannungsniveaus. Nicht wenige Finite-Elemente-Modelle (FEM) basieren auf dieser Grundlage. Das Problem: Nichts ist wirklich vollständig linear. Zweifellos gibt es viele Fälle, in denen die Linearitätsannahme geeignet ist, die Leistung zu modellieren und die Sicherheit und allgemeine Eignung ausreichend festzustellen. Es gibt aber auch Fälle, in denen das nicht zutrifft. Sowie weitere Fälle, in denen das Erzwingen höherer Leistung und Effizienz auf der Basis der neuesten und besten Designvariante ein tieferes Verständnis der zugrunde liegenden Physik und Prozesse erfordert.
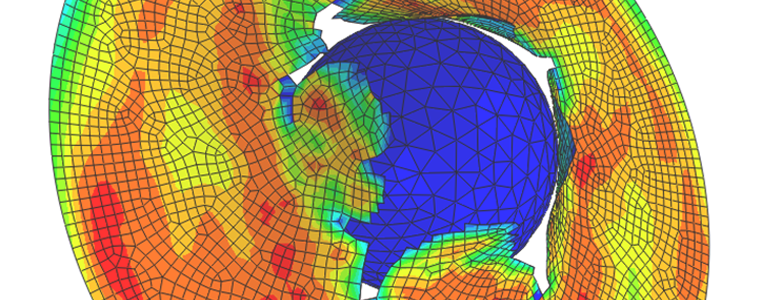
Abbildung einer nichtlinearen Analyse
Was bedeutet linear im FEM?
Um ein numerisches oder auch nur mentales Modell eines Systems oder einer Komponente zu erstellen, ist es erforderlich, einige Vereinfachungen vorzunehmen. Dinge, die Sie nur vermuten, sind nicht von Belang, und Dinge, die Sie eliminieren, ermöglichen einen besseren Einblick in das, was vor sich geht. Und in der Strukturmechanik werden Sie hauptsächlich die nichtlinearen Elemente eliminieren. Sie gehen von der Annahme aus, dass eine Verdopplung der Last zu einer Verdopplung der Durchbiegung führt und dass eine Verdopplung der Durchbiegung eine Verdopplung des Spannungsniveaus zur Folge hat. Bisher wurden die meisten Finite-Elemente-Modelle (FEM) auf der Grundlage dieser Annahmen erstellt.
Das Problem mit der großen Linearitätsannahme ist, dass sie einfach nicht zutrifft. Nichts ist wirklich vollständig linear. An diesem Punkt kann ich schon die Leute unter anderem sagen hören, dass diese Annahme doch bisher gut genug gewesen sei. Bis zu einem gewissen Grad ist das auch richtig. Es gibt viele Fälle, in denen die Linearitätsannahme mehr als geeignet ist, die Leistung zu modellieren und die Sicherheit und allgemeine Eignung ausreichend festzustellen. Es gibt aber auch Fälle, in denen das nicht zutrifft, und weitere Fälle, in denen das Erzwingen höherer Leistung und Effizienz auf der Basis der neuesten und besten Designvariante ein tieferes Verständnis der zugrunde liegenden Physik und Prozesse erfordert. Diese bewirken, wie sich das Ding dann tatsächlich verhält.
Niemand startet ohne sehr guten Grund eine nichtlineare Simulation, aber gute Gründe dafür gibt es viele. Und es lohnt sich.
Dieses ist vielleicht nicht das richtige Medium, um detaillierte Abhandlungen zur nichtlinearen Reaktion von Systemen und Komponenten zu verfassen. Es ist aber wahrscheinlich angebracht, ein paar Faktoren zu betrachten, die die vereinfachte lineare Seite verderben. Lassen Sie uns also mit den Materialien beginnen.
Was bedeutet nichtlinear im FAE?
Jeder hat an einem gewissen Punkt schon Erfahrungen mit nichtlinearen Materialien gemacht. Nehmen Sie ein Gummiband und ziehen Sie daran. Am Anfang erfordert es ein wenig Mühe, es zu dehnen. Dann plötzlich erreichen Sie mit nur wenig zusätzlicher Anstrengung jede Menge Bewegung. Ziehen Sie noch ein wenig weiter daran, und der Widerstand scheint wieder größer zu werden.
Die Reaktion des Materials ist eine Funktion der Belastung, der es bisher schon ausgesetzt war. Etwas Ähnliches passiert, wenn Sie ein Stück Stahl einer zu hohen Belastung aussetzen. Wenn Sie dies tun, wird nicht nur die Reaktion des Materials nichtlinear, es wird auch dauerhaft deformiert. In dem Teil der Reaktion, die nichtlinear und für die dauerhafte Verformung verantwortlich ist, wird eine Menge Energie absorbiert – eine gute Nachricht, wenn Sie einen Autounfall haben oder KFZ-Mechaniker sind. Das Interessante ist, wie Sie diese Merkwürdigkeit in einem CAE-Programm abbilden. Aber das ist ein Thema für einen anderen Ort und einen anderen Zeitpunkt.
Aber nicht nur Materialien verderben die lineare Seite. Die Art und Weise, in der Teile miteinander interagieren – Kontakt im FEA-Jargon – ist eine weitere Quelle der Nichtlinearität, wie auch eine hohe Durchbiegung oder eine Änderung der Form. Fügen Sie noch eine schnelle dynamische Belastung hinzu und Sie können die ganze Palette physikalischer Effekte beobachten, die dazu führen, dass die Durchbiegung ihre direkte Beziehung zur Belastung verliert.
Es ist ein weit verbreiteter Irrtum, dass Simulationssysteme wissen, wie sie diese Faktoren zu berücksichtigen haben, wenn man es ihnen nicht erzählt. Das tun sie nicht und können es wahrscheinlich in einem beliebigen praktischen Szenario auch gar nicht. In der Nachbetrachtung ist es zumindest offensichtlich, dass nichtlineare Simulationen nicht ohne Probleme durchzuführen sind und einfache, harte Arbeit erfordern. Aber was erhalten wir als Belohnung dafür? Zunächst einmal Produkte, die effektiver und vorhersagbarer in einem breiteren Anwendungsbereich funktionieren. Am Ende aber vor allem eines: Mehr Wissen über das Produkt. Und das ist sicherlich die größte Belohnung für einen Konstrukteur.
Der Vorteil der nichtlinearen Analyse
Ein Knackpunkt bei der linearen Analyse ist schlicht und einfach das Material. Das weiß jeder, der schon einmal ein Gummiband lang und länger gezogen hat. Die Reaktion des Materials ist eine Funktion der Belastung, der es bisher schon ausgesetzt war. Etwas Ähnliches passiert, wenn Stahl einer zu hohen Belastung ausgesetzt wird: Die Reaktion des Materials wird nichtlinear (und es wird dauerhaft deformiert). Die Interaktion von Komponenten, also ihr Zusammentreffen, stellt eine weitere Quelle der Nichtlinearität dar. Die Berücksichtigung solch wichtiger Faktoren ist keinesfalls traditioneller Standard bei Simulationssystemen. Und das nicht ohne Grund: Wie beschrieben, reicht in vielen Fällen der lineare Ansatz – in anderen allerdings stößt er an seine Grenzen. Nichtlineare Ansätze stießen in der Vergangenheit auf Ablehnung im Arbeitsalltag, weil ihre Umsetzung in der Tat kompliziert und langatmig – kurz: wenig praktikabel war. Inzwischen aber sorgt leistungsfähige Software für mehr Akzeptanz hinsichtlich der nicht-linearen FEA. Gerade bei einer Häufung nichtlinearer Herausforderungen durch das Produktportfolio („Knicken“, komplexes Material etc.) ist eine Software mit integrierter nicht-linearen Analyse das Mittel der Wahl. Sie erhöht unter anderem das Maß an Qualität, Sicherheit und Kostenersparnis.
Nichtlineare Simulations-Lösung Abaqus
Ein Beispiel für eine hochleistungsfähige FEA-Simulationslösung ist SIMULIA Abaqus Unified FEA. Sie hat sich bewährt bei komplizierten nichtlinearen Problemen sowie umfangreichen linearen Dynamikanalysen. Routineaufgaben erledigt sie gleichfalls souverän. Mit der Abaqus Simulation Software lassen sich unter anderem vollständige Fahrzeuglasten, dynamische Vibrationen, Crash, Mehrkörpersysteme, nichtlineare Statik, thermische Kopplung und akustisch-strukturelle Kupplung mit nur einer Modellierungsdatenstruktur und integrierter Solver-Technologie betrachten.
Häufige Fragen zu FEM /FEA:
Welche Prozesse werden mit FEM/FEA durchgeführt?
Die Finite Elemente Analyse, kurz FEM, zeigt als computergestütztes Verfahren die Reaktionen eines geplanten Produkts (Bauteil, Bauwerk etc.) auf physikalische Einwirkungen am Bildschirm. Beispiele dafür sind unter anderem Verformungen und Erhitzung.
Was sind die Vorteile von FEM/FEA?
Realistische Simulationen verringern die Zahl der notwendigen realen Prototypen – und damit auch der Kosten. Ein weiterer Vorteil ist das Plus an Qualität und Sicherheit durch Absicherung der Bauteileigenschaften.
Was spricht für die nichtlineare Analyse?
Die nichtlineare Analyse liefert auch bei komplexen Anforderungsprofilen ein Gesamtbild, während sich die lineare Analyse nur für Standardberechnungen eignet. Dank moderner Software ist der Aufwand für die nichtlineare Analyse nicht mehr ungleich höher als früher.